さて、ピタゴラスの定理から円錐の稜線の長さは y2 = 252 + 68.752　となるので、

y = 73となりました。また、円錐の仮想部分の稜線の長さは相似から、73:25=z:16なのでz = 46.72となります。

　円錐の底面の円周の長さは、 2πrなので 2 x 25 x π = 157 となります。

　円錐の側面を展開すると、稜線を半径とする円になるので、その半径は73となります。よってその円の円周は 73 x 2 x π = 459 です。

　したがって、円錐の側面を展開したときの角度は、157 ÷ 459 x 360 = 123°となります。

 
 

　続いて、第一展望台の製図です。

　下が直径32mの正円、上が直径50mの正円とのことなので、下図のような円錐の一部ということになります。下が高さ342m、上が高さ375mとのことなので、展望台の厚みは33mということになります。ただ下図のごとく、円錐が2個重なったような形をしており、写真から測定すると下図のような厚みということになりました。

　ここで、おっと、機械室というのがありました。機械室は、上下水道の中継やポンプがあるそうです。展望台が高い位置にあるから、水道が大変そうです。150mと250mの位置にありますが、外からは黒っぽく見えて実体はよくわかりませんので、黒っぽく作ることにしました。

　段ボールを幅2cm程度に切って、マジックで黒くぬり、スカイツリーの中に押し込んで、ちょうど良い位置でアロンアルファで固定しました。天井がないとかっこわるいので目測で段ボールをちょうど良い形に切って、こちらは銀色にぬり、中に押し込んでグルーガンで先の段ボールと固定しました。

25m

16m

33m

8.25m

24.75m

x

円錐の仮想部分の高さをｘとすると、相似関係から

(24.75+x) : 25 = x : 16

ということになります。

　よって、x = 44となりましたので、全体として円錐の高さは68.75となります。

y

さて、ピタゴラスの定理から円錐の稜線の長さは y2 = 252 + 68.752　となるので、

y = 73となりました。また、円錐の仮想部分の稜線の長さは相似から、73:25=z:16なのでz = 46.72となります。

　円錐の底面の円周の長さは、 2πrなので 2 x 25 x π = 157 となります。

　円錐の側面を展開すると、稜線を半径とする円になるので、その半径は73となります。よってその円の円周は 73 x 2 x π = 459 です。

　したがって、円錐の側面を展開したときの角度は、157 ÷ 459 x 360 = 123°となります。

z

157

123°

123°

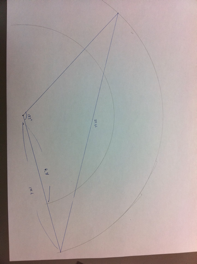
　分度器だけだと不正確なので、下図のように考えると、aの長さは円の直径73に対する61.5°の正弦となるので、 a= 73 x sin 61.5°　となりますので　a=64.15　です。

a

これを1/500で作図すると、64.15mの2倍は1/500では29.2cmに相当するので、その弦がその長さになる位置をさがすと、ちょうど123°となりました。

0.5mmアクリル板をこの大きさにカットし、おおよそで窓の高さを決めて、銀色のマジックで塗装。透けるので裏表とも塗装。

0.5mmアクリル板をこの大きさにカットし、おおよそで窓の高さを決めて、銀色のマジックで塗装。透けるので裏表とも塗装。これを丸めてセメダインで接着。段ボールで天井と床をつくり、銀色に塗装しました。真ん中には中塔が通る大きさの穴を開けました。同じ大きさのものをもう一つ作り、上の二重の円錐部分を作成。これを上にグルーガンで接着して、第一展望台の完成です。